
Veškeré zde vystavené nákresy byly vykresleny pomocí programu QCAD. Celý výrobek jsme konstrukčně rozdělili na šest částí:
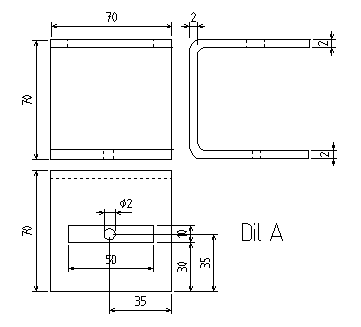
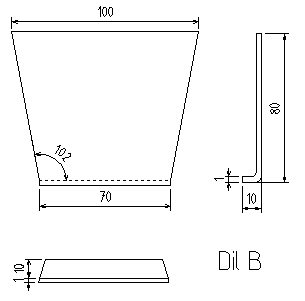
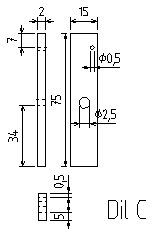
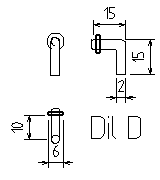
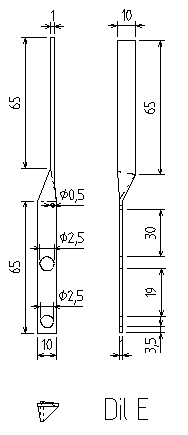
Jejich složení je schématicky znázorněno na tomto obrázku: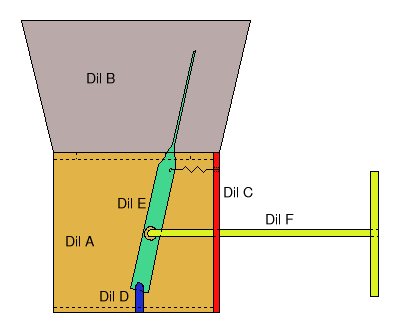
Odkazy na DXF soubory: Díl A, Díl B, Díl C, Díl D, Díl E, Díl F, Celek.
Pro výrobu naší měřící aparatury budeme potřebovat polymetylmetakrylát (PMMA, plexisklo), plech, drát, pružina, lepidlo. Jedná se většinou o věci, které se v dílně vždycky nějak najdou, ale celkově by cena výrobku neměla překročit cca 70 Kč. Potřebné nářadí: vrtačka, nůžky na plech, pilku na železo, opalovačka, pilník.
Náš přístroj je založen na principu měření (resp. reakce na) odporové síly, vznikající při obtékání tělesa reálnou tekutinou.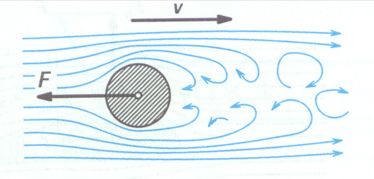 Obtékání těles je složitý děj, při kterém dochází k přemisťování mnoha částic tekutiny vzhledem k povrchu tělesa. Částice tekutiny interagují s částicemi obtékaného tělesa za vzniku odporové síly v důsledku vnitřního tření mezi částicemi, přičemž odporová síla působí proti směru relativního pohybu tělesa v tekutině. U kapalin se jedná o tzv. hydrodynamickou odporovou sílu, u plynů pak o odporovou sílu aerodynamickou, celkově je tento jev označován jako odpor prostředí.
Obtékání těles je složitý děj, při kterém dochází k přemisťování mnoha částic tekutiny vzhledem k povrchu tělesa. Částice tekutiny interagují s částicemi obtékaného tělesa za vzniku odporové síly v důsledku vnitřního tření mezi částicemi, přičemž odporová síla působí proti směru relativního pohybu tělesa v tekutině. U kapalin se jedná o tzv. hydrodynamickou odporovou sílu, u plynů pak o odporovou sílu aerodynamickou, celkově je tento jev označován jako odpor prostředí.
Velikost této odporové síly je přímo úměrná jedné polovině hustoty r kapaliny obtékající těleso, obsahu S styčné plochy tělesa, druhé mocniny rychlosti v tekutiny a koeficientu C, který je závislý na tvaru obtékaného tělesa. Matematicky vyjádřeno má tedy tento vztah následující tvar (jeho odvození viz kapitola 3.b):
![F=1/2CSv^2[ro]](img/vzorce/odpor1.gif) , (1)
, (1)
přičemž pro rychlost odvodíme následující vztah:
![v=sqrt(2F/CS[ro])=sqrt(F/[alfa])](img/vzorce/odpor2.gif) . (2)
. (2)
Jaký však je tento zákon ve své podstatě? Je analogický s F = ma? Není a ani být nemůže, protože tento zákon je v první řadě empirický, odvozený na základě zkoušek v aero(hydro)dynamickém tunelu a je výsledkem mnoha spolu souvisejících jevů a ne v podstatě jedné věci, jako je tomu u F = ma. Čím hlouběji ho budeme zkoumat a čím podrobnější měření provedeme, tím se zákon bude stávat komplikovanější či jinak řečeno zjistíme, že je chybnější a chybnější. Jeho největší vadou je závislost na velikosti rychlosti tekutiny obtékající těleso. Zatímco při (velmi) malých rychlostech vzrůstá velikost odporové síly spíše lineárně, při středních rychlostech je tato závislost přímo úměrná druhé mocnině rychlosti a při vysokých rychlostech, např. při rychlostech vyšších než je rychlost zvuku, kdy kolem tělesa vzniká tzv. rázová vlna, způsobující silné zvukové třesky při přeletu nadzvukových letadel, již zákon ve tvaru druhé mocniny rychlosti selhává a odporová síla je úměrná třetí mocnině rychlosti. Je to v důsledku rozložení proudnic kolem obtékaného tělesa. Při menších rychlostech se jedná o tzv. proudění laminární, zatímco při velkých rychlostech vzniká tzv. proudění turbulentní se zpětnými víry (nastává u vody a vzduchu, ale např. med zpětné víry nevytváří).
Dalším problémem je určení koeficientu C obtékaného tělesa, který závisí na tvaru tělesa. Pro základní tvary (dutá polokoule, vypouklá polokoule, koule, těleso proudnicového tvaru) byl tento koeficient přibližně určen při pokusech v aerodynamickém tunelu. Pro nás však obě tyto potíže nehrají příliš velkou roli, protože při konstrukci našeho přístroje jsme si jako obtékané těleso zvolili čtvercovou destičku s dobře známým koeficientem 1,10 a vzhledem k tomu, že náš přístroj také pravděpodobně nebude používán za extrémně vysokých rychlostí proudící tekutiny, odpadá i problém se závislostí na velikosti rychlosti kapaliny. Velkou výhodou našeho přístroje je také fakt, že sestavení jeho stupnice pro měření rychlosti vychází přímo z experimentu, čímž se celá situace velmi zjednodušuje. Odpadá totiž problém mechanického převodu velikosti odporové síly na výslednou rychlost proudící kapaliny. Odporovou sílu díky zvolenému mechanismu vůbec nepotřebujeme znát. Při experimentu byla použita soustava s proudící vodou, přičemž rychlost jejího proudění jsme znali. Při této známé rychlosti jsme tedy zjistili, jak moc se ručička našeho „měřáku“ vychýlila a tento úsek jsme na budoucí stupnici zaznamenali. Získali jsme tak velikost jednoho dílku stupnice, který odpovídá rychlosti proudící vody v použité aparatuře. Jak je však patrno z předchozích úvah, stupnice nebude lineární. Její popis není v žádném případě triviální, a proto je vždy zapotřebí aparaturu kvalitně zkalibrovat.
Pohybuje-li se těleso kapalinou (nebo naopak kapalina těleso obtéká), pak na těleso působí odporová síla způsobená dvěma faktory:
![Fv=1/2Sv[ro]v^2](img/vzorce/odpor3.gif) ,
, ![F=1/2S[ro]v^2](img/vzorce/odpor4.gif) ,
, ![F'=6[pí][eta]rv](img/vzorce/odpor5.gif) ,
,Ve skutečnosti však obě příčiny vždy působí zároveň a proto obecná závislost odporu prostředí F na rychlosti v má tvar:
F = Av2 + Bv .
Při velikých rychlostech převládá tedy kvadratický člen a naopak při velmi malých rychlostech převládá lineární člen. I my jsme jej zanedbali, neboť pro malé rozměry tělesa si tuto nepřesnost můžeme dovolit.
Pro zjednodušení výpočtu se tedy lineární člen často zanedbává, ale zároveň se zavádí tvarový součinitel C, který vypovídá o tvaru tělesa. Získáváme tedy upravený Newtonův vztah:
![F=1/2CSv^2[ro]](img/vzorce/odpor1.gif) .
.
Pro naše použití jsme zvolili čtvercovou destičku, pro níž platí C = 1,10.
Ačkoliv by se mohlo zdát, že zkalibrovat naši aparaturu nebude žádný velký problém, realita nebyla úplně shodná s touto tezí. Kvůli nemožnosti otestovat náš přístroj v laboratorních podmínkách,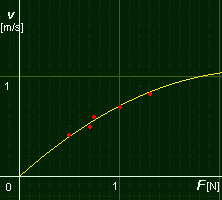 neboť se nevešel do našeho experimentálního korýtka, jsme byli nuceni vydat se přímo do terénu. Využili jsme přitom již zkalibrované trubičky, která nám tedy posloužila jako měřič rychlosti vody v klatovském Drnovém potoce. Samotné měření bylo pak vcelku snadné, avšak voda již nebyla nejteplejší. Bohužel.
neboť se nevešel do našeho experimentálního korýtka, jsme byli nuceni vydat se přímo do terénu. Využili jsme přitom již zkalibrované trubičky, která nám tedy posloužila jako měřič rychlosti vody v klatovském Drnovém potoce. Samotné měření bylo pak vcelku snadné, avšak voda již nebyla nejteplejší. Bohužel.
Jak jsme tedy postupovali? Nejprve jsme si zvolili vhodné místo, kde jsme změřili rychlost proudící vody pomocí trubičky. Následně jsme aplikovali náš siloměr. Kolik ukázala ručička, tolik jsme označili na stupnici. Po návratu do laboratoře jsme pomocí siloměru určili sílu, kterou voda působila při daných rychlostech. Tato data jsme zanesli do grafu a provedli regresní analýzu. Získali jsme tím koeficient ?, a tak jsme mohli další hodnoty výchylek ručičky/rychlostí vody již dopočítat. Ze vzniklého grafu jsme se mohli přesvědčit o tom, že pro malé rychlosti je závislost odporové síly na rychlosti spíše lineární, zatímco pro vyšší hodnoty je již kvadratická (viz článek 3.a).
Vzhledem k našim technickým možnostem jsme byli nuceni aparaturu stavět jenom jako použitelnou demoverzi. Pokud by se takové zařízení mělo skutečně používat, bylo by třeba především provést důkladnější kalibraci. Dále jsme uvažovali o sérii různých vyměnitelných pružin pro různě rychlé toky. Tím by se výrazně rozšířila použitelnost zařízení pro prakticky libovolné toky. Avšak by bylo zapotřebí vždy použít jinou stupnici.
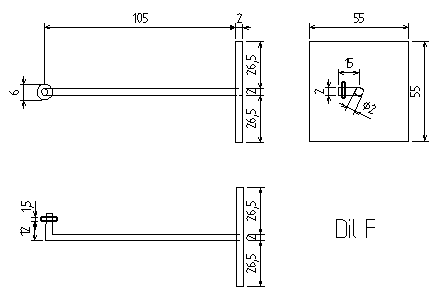
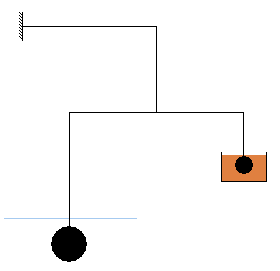 Další naše úvahy k využití odporové síly pro měření rychlosti již směřovaly k využití torzní mechaniky. Jedná se o nejpřesnější způsob mechanického měření, čili by se tak daly pozorovat i jen velmi malé rozdíly rychlostí. Schéma takového přístroje můžete vidět na obrázku vpravo. Jedna koule by byla vždy ponořená ve vodě a druhá v nějaké jiné kapalině o vyšší viskozitě (zpravidla olej). Odporová síla by se pak snažila dolní částí otáčet. Proti ní by ale působila odporová síla koule v oleji a drátu, který se nechce kroutit. Měření by probíhalo tak, že by se změřil úhel, o který se dolní část vychýlila a tento výsledek by se pak přepočítal na rychlost.
Další naše úvahy k využití odporové síly pro měření rychlosti již směřovaly k využití torzní mechaniky. Jedná se o nejpřesnější způsob mechanického měření, čili by se tak daly pozorovat i jen velmi malé rozdíly rychlostí. Schéma takového přístroje můžete vidět na obrázku vpravo. Jedna koule by byla vždy ponořená ve vodě a druhá v nějaké jiné kapalině o vyšší viskozitě (zpravidla olej). Odporová síla by se pak snažila dolní částí otáčet. Proti ní by ale působila odporová síla koule v oleji a drátu, který se nechce kroutit. Měření by probíhalo tak, že by se změřil úhel, o který se dolní část vychýlila a tento výsledek by se pak přepočítal na rychlost.
Více fotografií najdete ve fotogalerii.
Vzhledem k výše popsaným podmínkám naše zařízení měří jen rychlosti do 1 m/s. Avšak tento nedostatek lze odstranit změnou tuhosti pružiny.
[1] RNDr. Milan Bednařík, CSc., doc. RNDr. Miroslava Široká, CSc., ing. Petr Bujok: Fyzika pro gymnázia: Mechanika; Prometheus 1994
[2] Prof. Ing. Dr. Otakar Maštovský: Hydromechanika pro strojní inženýry; Státní nakladatelství technické literatury, 1955
[3] NASA: http://www.grc.nasa.gov/WWW/K-12/airplane/bga.html